Fórmula dos Juros Compostos e Como Utilizá-la
A fórmula para calcular os juros compostos é a seguinte:
M = C × (1 + i)t
Nessa fórmula, temos:
- M: o montante final, ou seja, o valor acumulado ao fim do
período;
- C: o capital inicial investido ou emprestado;
- i: a taxa de juros (em formato decimal);
- t: o tempo que o capital permanecerá aplicado ou o período do
empréstimo.
Ao usar essa fórmula, é essencial que o período de tempo e a taxa de juros estejam na mesma unidade. Por
exemplo, se a taxa de juros é mensal, o tempo também deve ser em meses. Assim, para um cálculo de 24 meses,
o valor correto a inserir para t é 24, e não 2 (anos).
Para transformar a taxa de juros em formato decimal, basta dividir a porcentagem por 100. Dessa forma, 5% ao
mês torna-se 0,05.
Exemplo Prático
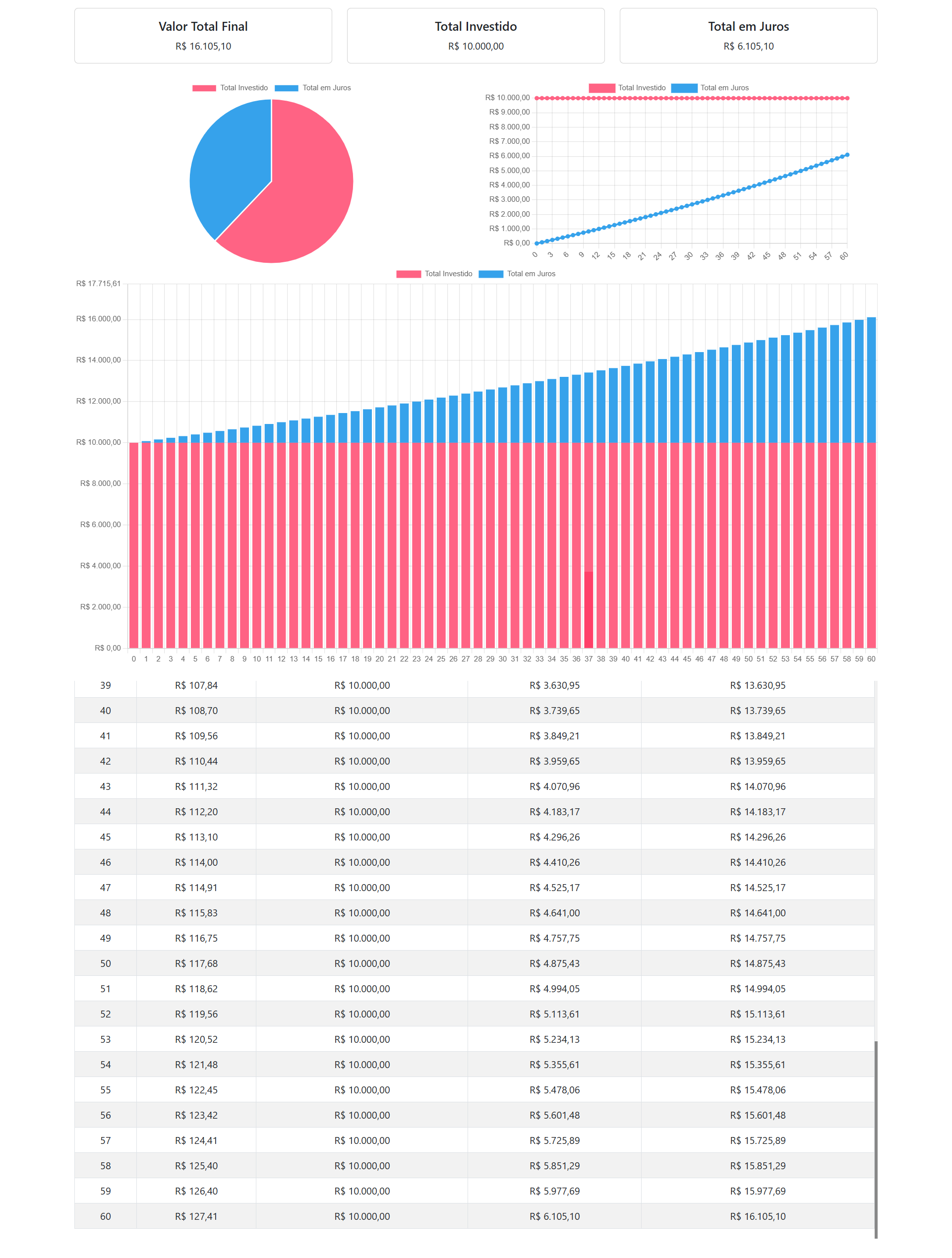
Suponha um investimento inicial de R$10.000,00, com uma taxa de juros de 10% ao ano, ao longo de 5 anos.
- No primeiro ano, a aplicação rende 10% sobre R$10.000,00, gerando R$1.000,00 e
acumulando um total de R$11.000,00.
- No segundo ano, o rendimento de 10% se aplica sobre R$11.000,00, aumentando para
R$12.100,00.
- Ao final de cinco anos, o montante total será de R$16.105,10.
Em comparação com juros simples, os juros compostos trazem um crescimento exponencial ao saldo, enquanto no
juros simples os ganhos permanecem fixos. Ao longo do tempo, o efeito dos juros compostos pode fazer uma
grande diferença, seja aumentando seus rendimentos ou o valor devido em dívidas.
O impacto dos juros compostos nas finanças pessoais
Os juros compostos são uma das ferramentas mais poderosas no mundo das finanças. Diferentemente dos juros
simples, onde a taxa incide apenas sobre o capital inicial, nos juros compostos o cálculo é feito sobre o
montante acumulado, incluindo os juros acumulados ao longo do tempo.
Como os juros compostos afetam empréstimos e investimentos
O uso dos juros compostos é comum tanto em empréstimos quanto em investimentos. Eles proporcionam um
crescimento exponencial, mas a direção desse crescimento – seja a seu favor ou contra você – depende da
posição em que você está.
Ao tomar um empréstimo, como um financiamento de imóvel, os juros compostos podem elevar
significativamente o valor final a ser pago, pois a cada mês o saldo aumenta. Isso significa
que o valor da dívida pode crescer rapidamente se não houver pagamentos frequentes.
O uso de juros compostos também é comum em dívidas de cartão de crédito. Cada vez que a
fatura não é quitada, os juros compostos são aplicados sobre o saldo total, o que pode
transformar pequenas dívidas em grandes preocupações financeiras.
Em contrapartida, ao investir com juros compostos, você permite que o dinheiro trabalhe a seu
favor. Investimentos como CDBs, LCI, Tesouro Direto e fundos de investimento de longo prazo
geralmente oferecem rendimentos baseados em juros compostos. Nesse caso, o valor investido
cresce exponencialmente com o tempo, o que permite uma acumulação de capital mais
significativa.
Diferenças entre juros simples e compostos
-
Juros Simples: Calculados apenas sobre o capital inicial. Forma uma progressão linear
de crescimento. Benefícios são constantes ao longo do tempo.
-
Juros Compostos: Calculados sobre o montante acumulado. Crescimento exponencial e curva
ascendente. Oferece potencial para maiores ganhos a longo prazo.
Exemplo prático de juros compostos em investimentos
Imagine que você invista R$ 10.000 com uma taxa de 8% ao ano, aplicada ao longo de 10 anos. No regime de
juros compostos, o montante acumulado será significativamente maior do que no regime de juros simples. Ao
final de uma década, a diferença entre os dois tipos de cálculo seria considerável, destacando a importância
dos juros compostos no crescimento do patrimônio.
A mágica dos juros compostos
Os juros compostos podem parecer complexos, mas a ideia é simples: quanto mais tempo o capital permanece
investido, maior é o efeito multiplicador. É esse efeito que permite que investidores construam patrimônio
de forma consistente ao longo do tempo, conforme descrito por Albert Einstein, que uma vez disse: “Os juros
compostos são a maior força do universo”.